Introdução

Os processos autoregressivos são um dos mais simples modelos estudados em séries temporais. Uma característica interessante é sua semelhança com os modelos de regressão. Por exemplo, o modelo autoregressivo de ordem \(1\), \(\mathrm{AR}(1)\), pode ser definido da seguinte forma \[\begin{equation}\label{eq:ar1} Y_t \sim N(\mu_t, \sigma^2), \quad \text{em que} \quad \mu_t = \alpha + \phi\,y_{t-1} \end{equation}\] para \(t = 1,\ldots,n.\) Note que \(y_{t-1}\) faz o papel das covariáveis e a variância é constante ao longo do tempo.

Este post tem objetivo apresentar uma implementação em R para simulação e estimação de um processo \(\mathrm{AR}(1)\). Embora já esteja implementado nas funções arima.sim e arima este exercício fornece uma compreensão da estrutura do modelo e consequentemente um caminho para implementações de modelos mais complexos.

Simulação

Os valores dos parâmetros para o modelo simulado são \(\alpha = -2.0\), \(\phi = 0.7\), \(\sigma^2 = 4.0\) e tamanho amostral \(n = 500\). Como a distribuição de probabilidade é a Normal então a função rnorm foi utilizada.

set.seed(666)
n <- 500
alpha <- -2.0
sigma <- 2.0
phi <- 0.7
y <- numeric(n)
for(t in 2:n) {
  mu_t <- alpha + phi * y[t-1]
  y[t] <- rnorm(1, mean = mu_t, sd = sigma)
}

Estimação

Dada uma amostra \(\mathbf{y} = (y_1, \ldots, y_n)\) do modelo \(\mathrm{AR}(1)\), sob a suposição de normalidade a verossimilhança do modelo é dada por \[ L(\mathbf{\theta} \mid \mathbf{y}) \propto (\sigma^2)^{-\frac{n}{2}}\,\exp\left\{-\frac{1}{2\,\sigma^2}\sum_{t=2}^{n}\left[y_t - (\alpha -\phi\,y_{t-1}) \right]^2 \right\} \] em que \(\mathbf{\theta} = (\alpha, \phi, \sigma^2)\).

A estimativa de máxima verossimilhança de \(\mathbf{\theta}\) é obtida numericamente maximizando a função log-verossimilhança.

log_like <- function(parms, y) {
  n <- length(y)

  phi <- parms[1]
  alpha <- parms[2]
  sigma <- parms[3]

  eta <- numeric(n)

  for(k in 2:length(y)) eta[k] <- phi * y[k-1]

  ll <- sum(dnorm(x = y, mean = eta + alpha, sd = sigma, log = TRUE))
  return(ll)
}

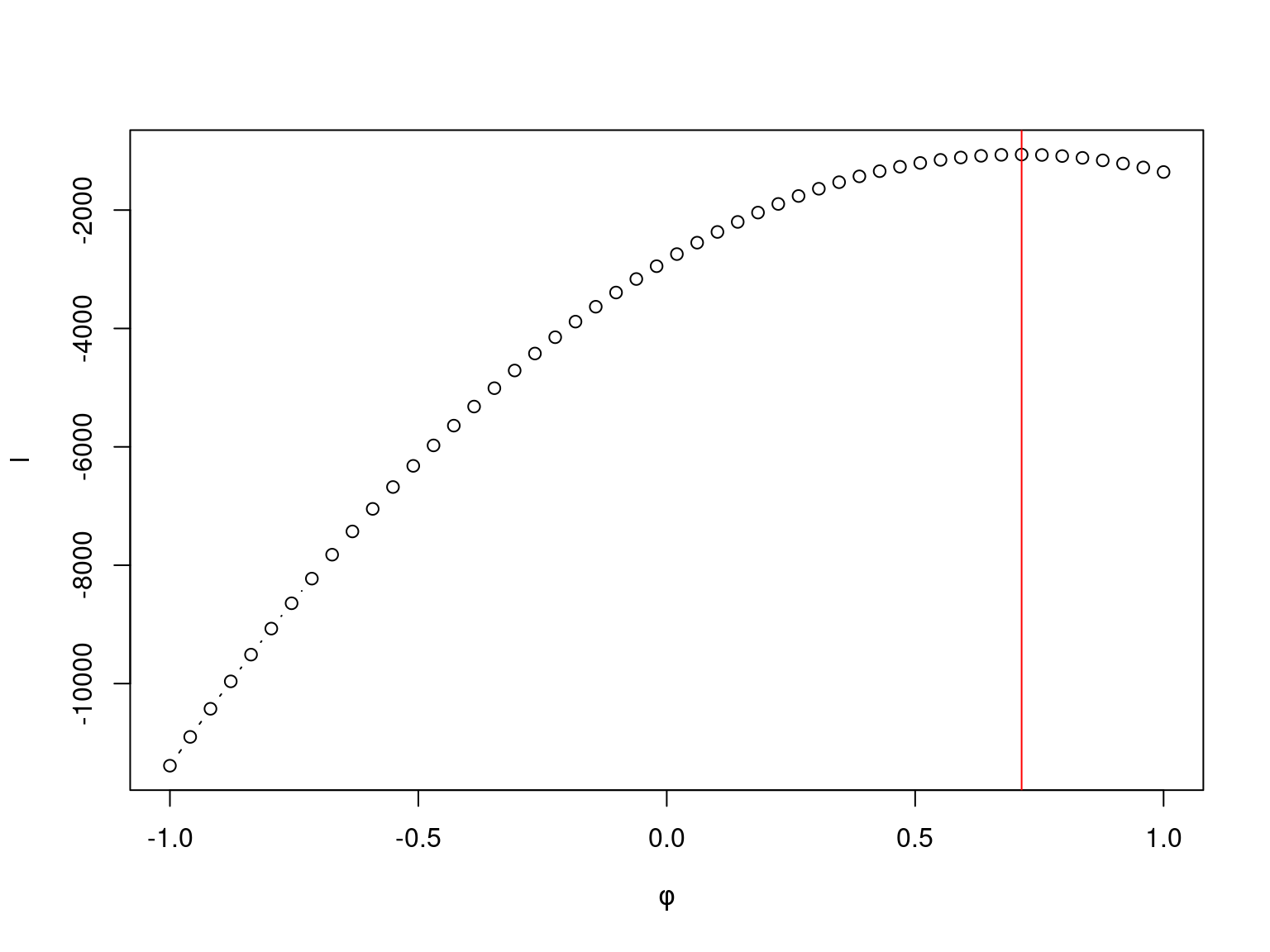
Para \(\alpha\) e \(\sigma^2\) fixos a função de verossimilhança perfilhada de \(\phi\) para os dados simulados tem o seguinte comportamento.

A maximização numérica da log-verossimilhança no R é realizada pela função optim. Neste caso, optei pelo método BFGS (method = "BFGS"), indiquei para maximizar a função (control = list(fnscale = -1)) e pedi para retornar a matriz hessiana (hessian = TRUE).

fit <- optim(par = c(phi, alpha, sigma), fn = log_like, y = y, method = "BFGS",
             control = list(fnscale = -1), hessian = TRUE)

As estimativas dos parâmetros \(\phi\), \(\alpha\) e \(\sigma\) foram, respectivamente,

## [1]  0.6997547 -2.0902103  2.0239194

muito próximas dos verdadeiros valores estipulados.

Note que os autovalores da matriz hessiana são negativos, portanto tais estimativas são de fato as estimativas de máxima verossimilhança.

eigen(fit$hessian)$values

## [1]   -17.22736  -244.12550 -6993.97570

Previsão

No modelo \(\mathrm{AR}(1)\) o valor predito no instante \(t\) é dado por \[ y_{t} = \hat{\alpha} + \hat{\phi}\,y_{t-1} \] em que \(\hat{\alpha}\) e \(\hat{\phi}\) são as estimativas de máxima verossimilhança.

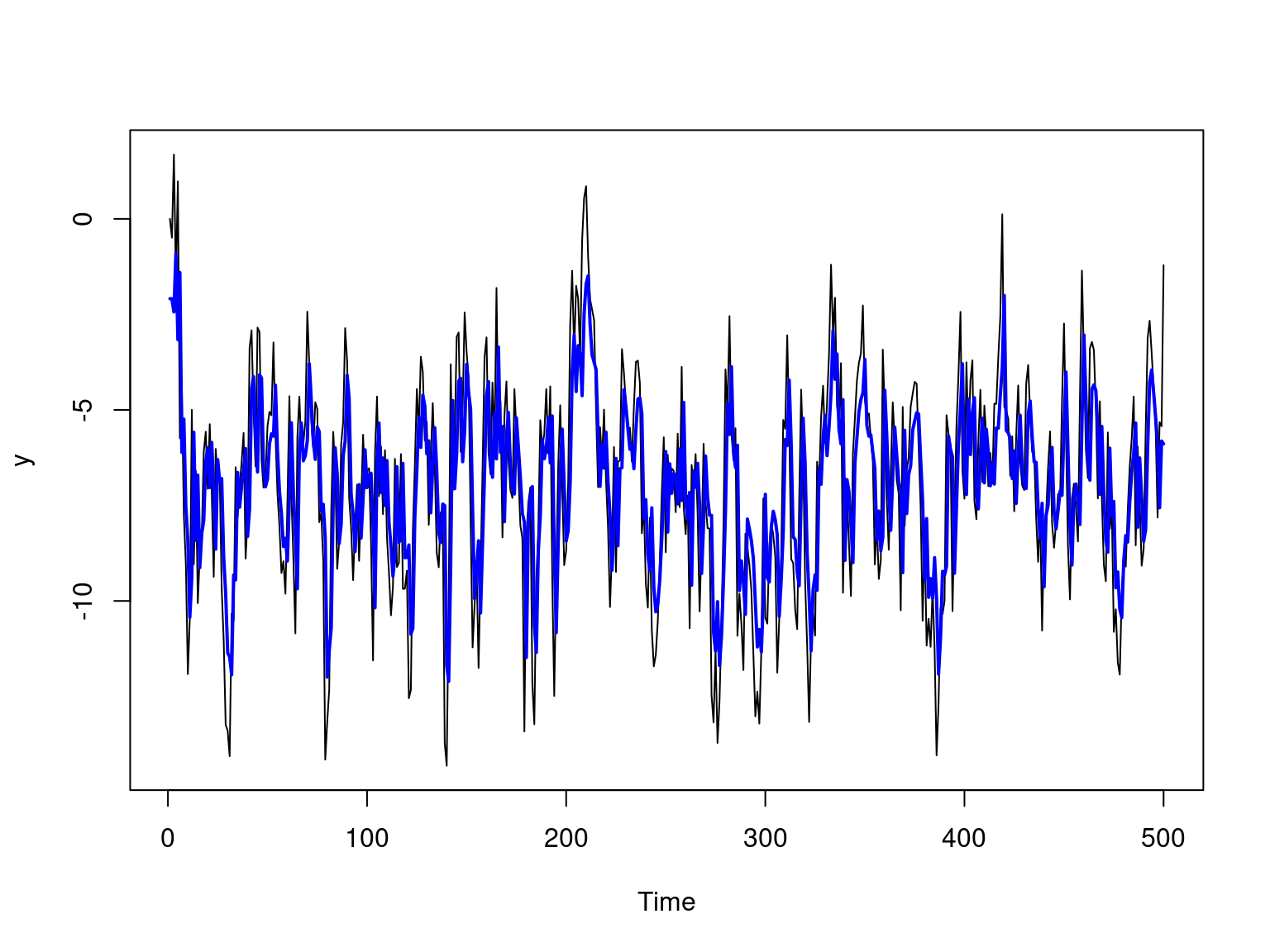
O gráfico abaixo apresenta a série observada sobreposta pela séria com os valores preditos.

mles <- fit$par
phi_hat <- mles[1]
alpha_hat <- mles[2]
sigma_hat <- mles[3]
yhat <- numeric(n)
for(t in 2:n) yhat[t] <- phi_hat * y[t-1]
ts.plot(y)
lines(yhat + alpha_hat, type = "l", col = "blue", lwd = 2)