Density function, distribution function, quantile function and random number generation function for the Log-extended exponential-geometric distribution reparametrized in terms of the \(\tau\)-th quantile, \(\tau \in (0, 1)\).
Usage
dleeg(x, mu, theta, tau = 0.5, log = FALSE)
pleeg(q, mu, theta, tau = 0.5, lower.tail = TRUE, log.p = FALSE)
qleeg(p, mu, theta, tau = 0.5, lower.tail = TRUE, log.p = FALSE)
rleeg(n, mu, theta, tau = 0.5)Arguments
- x, q
vector of positive quantiles.
- mu
location parameter indicating the \(\tau\)-th quantile, \(\tau \in (0, 1)\).
- theta
nonnegative shape parameter.
- tau
the parameter to specify which quantile is to be used.
- log, log.p
logical; If TRUE, probabilities p are given as log(p).
- lower.tail
logical; If TRUE, (default), \(P(X \leq{x})\) are returned, otherwise \(P(X > x)\).
- p
vector of probabilities.
- n
number of observations. If
length(n) > 1, the length is taken to be the number required.
Value
dleeg gives the density, pleeg gives the distribution function,
qleeg gives the quantile function and rleeg generates random deviates.
Invalid arguments will return an error message.
Details
Probability density function $$f(y\mid \alpha ,\theta )=\frac{\theta \left( 1+\alpha \right) y^{\theta -1}}{\left( 1+\alpha y^{\theta }\right) ^{2}}$$
Cumulative distribution function $$F(y\mid \alpha ,\theta )=\frac{\left( 1+\alpha \right) y^{\theta }}{1+\alpha y^{\theta }}$$
Quantile function $$Q(\tau \mid \alpha ,\theta )=\left[ \frac{\tau }{1+\alpha \left( 1-\tau\right) }\right] ^{\frac{1}{\theta }}$$
Reparameterization $$\alpha=g^{-1}(\mu )=-\frac{1-\tau \mu ^{\theta }}{\left( 1-\tau \right) }$$
References
Jodrá, P. and Jiménez-Gamero, M. D., (2020). A quantile regression model for bounded responses based on the exponential-geometric distribution. Revstat - Statistical Journal, 18(4), 415--436.
Examples
set.seed(123)
x <- rleeg(n = 1000, mu = 0.5, theta = 1.5, tau = 0.5)
R <- range(x)
S <- seq(from = R[1], to = R[2], by = 0.01)
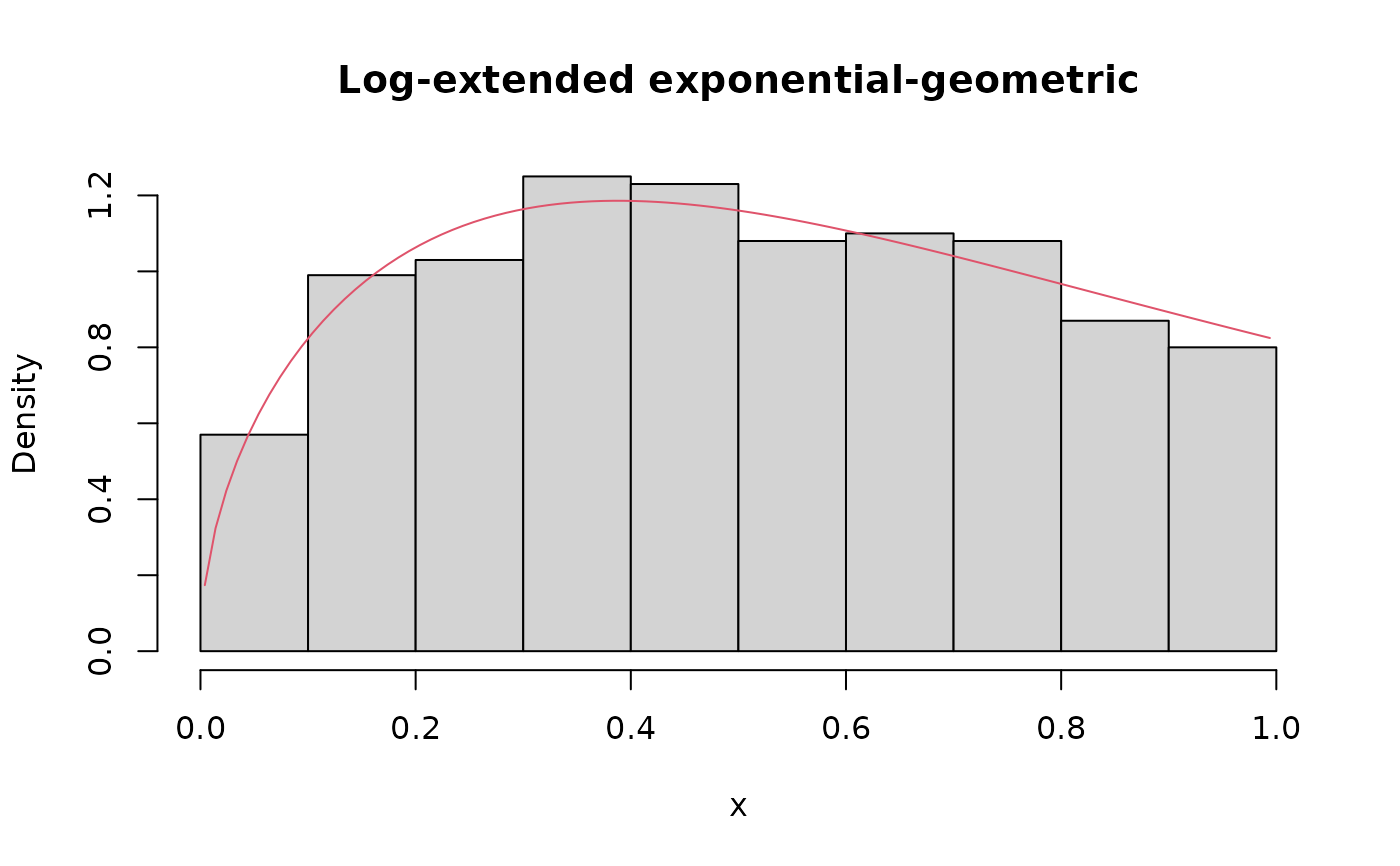
hist(x, prob = TRUE, main = 'Log-extended exponential-geometric')
lines(S, dleeg(x = S, mu = 0.5, theta = 1.5, tau = 0.5), col = 2)
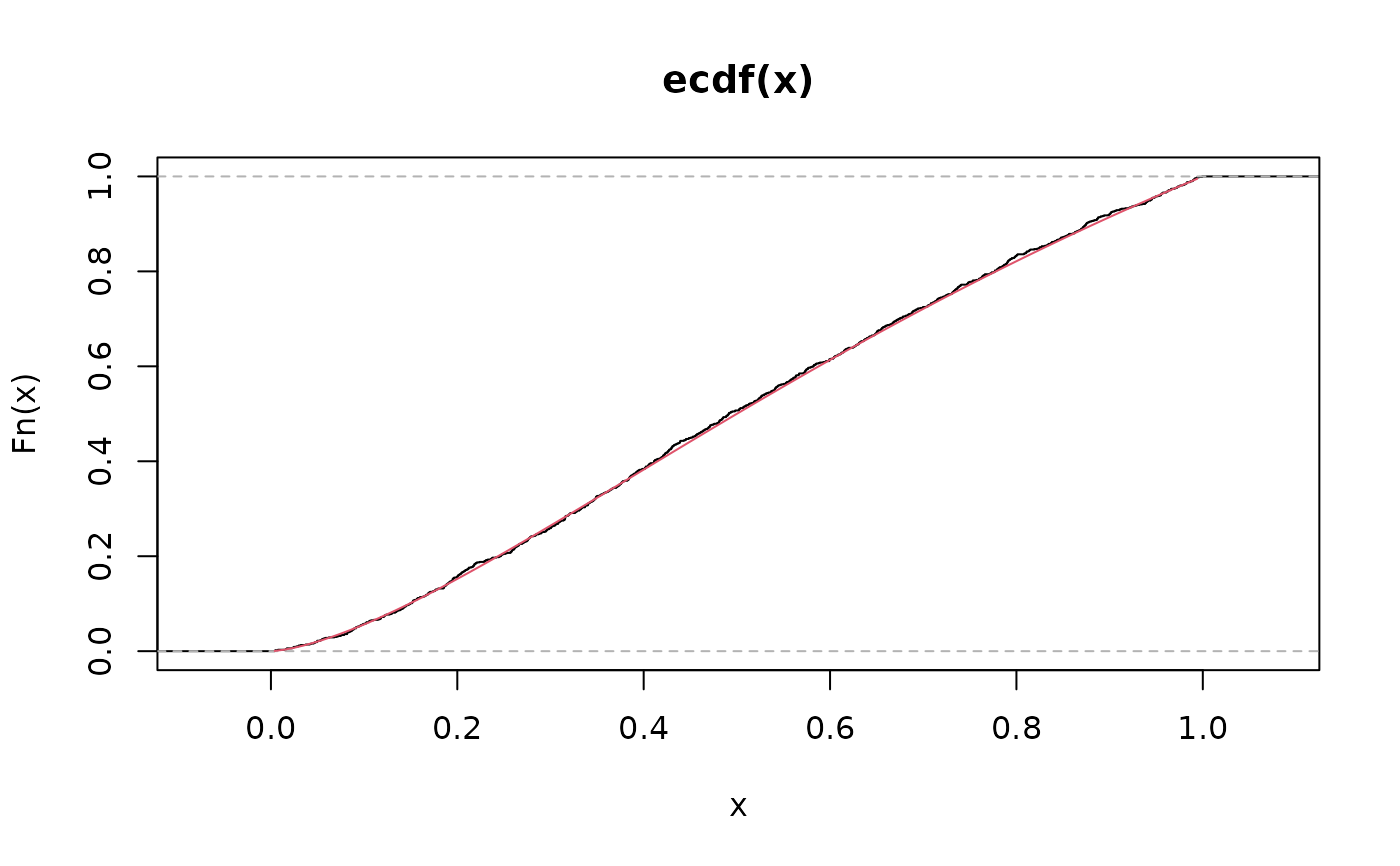
 plot(ecdf(x))
lines(S, pleeg(q = S, mu = 0.5, theta = 1.5, tau = 0.5), col = 2)
plot(ecdf(x))
lines(S, pleeg(q = S, mu = 0.5, theta = 1.5, tau = 0.5), col = 2)
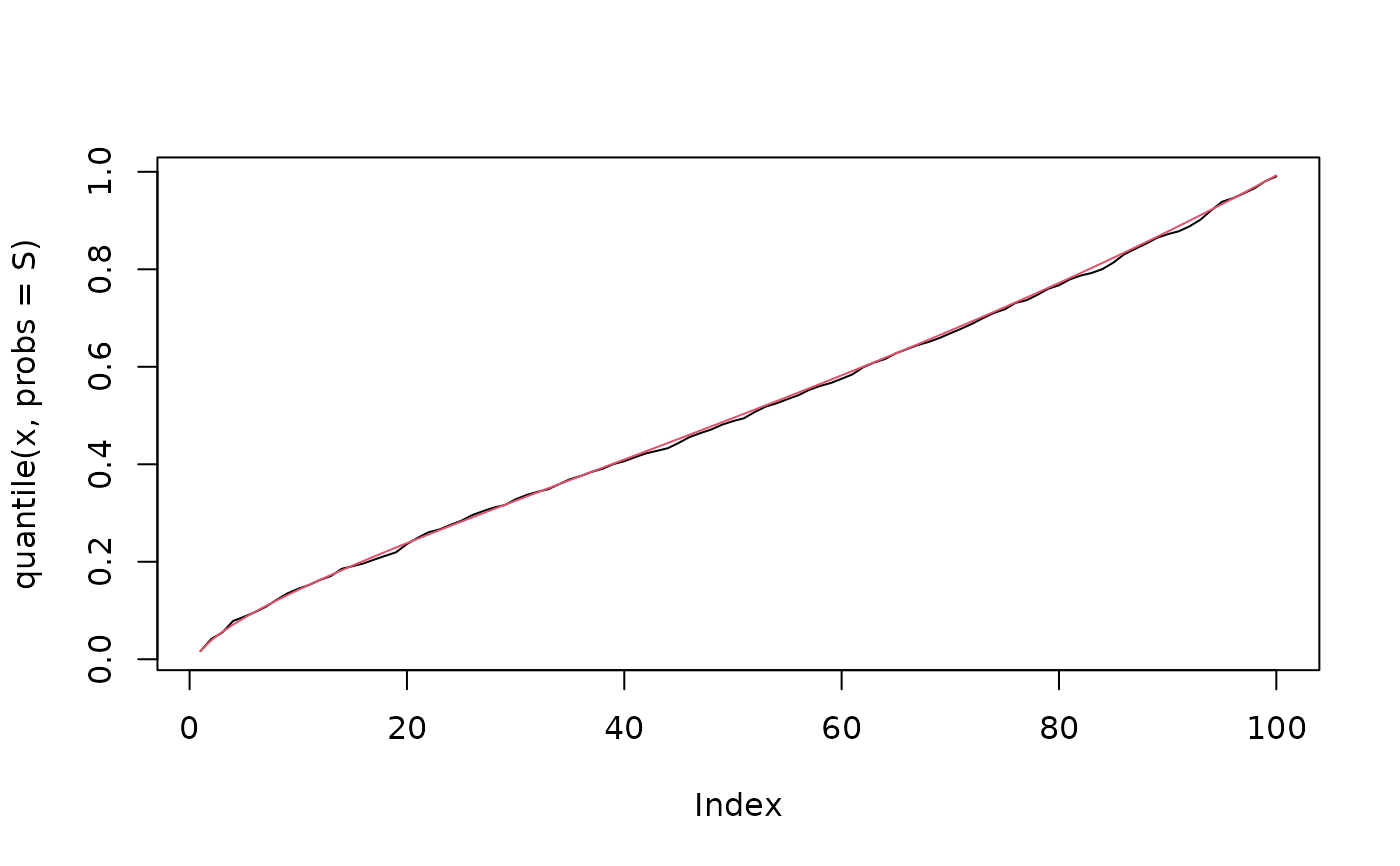
 plot(quantile(x, probs = S), type = "l")
lines(qleeg(p = S, mu = 0.5, theta = 1.5, tau = 0.5), col = 2)
plot(quantile(x, probs = S), type = "l")
lines(qleeg(p = S, mu = 0.5, theta = 1.5, tau = 0.5), col = 2)