Density function, distribution function, quantile function and random number generation function for the unit-Gumbel distribution reparametrized in terms of the \(\tau\)-th quantile, \(\tau \in (0, 1)\).
Usage
dugumbel(x, mu, theta, tau = 0.5, log = FALSE)
pugumbel(q, mu, theta, tau = 0.5, lower.tail = TRUE, log.p = FALSE)
qugumbel(p, mu, theta, tau = 0.5, lower.tail = TRUE, log.p = FALSE)
rugumbel(n, mu, theta, tau = 0.5)Arguments
- x, q
vector of positive quantiles.
- mu
location parameter indicating the \(\tau\)-th quantile, \(\tau \in (0, 1)\).
- theta
nonnegative shape parameter.
- tau
the parameter to specify which quantile use in the parametrization.
- log, log.p
logical; If TRUE, probabilities p are given as log(p).
- lower.tail
logical; If TRUE, (default), \(P(X \leq x)\) are returned, otherwise \(P(X > x)\).
- p
vector of probabilities.
- n
number of observations. If
length(n) > 1, the length is taken to be the number required.
Value
dugumbel gives the density, pugumbel gives the distribution function,
qugumbel gives the quantile function and rugumbel generates random deviates.
Invalid arguments will return an error message.
Details
Probability density function $$f(y\mid \alpha ,\theta )=\frac{\theta }{y(1-y)}\exp \left\{ -\alpha -\theta \log \left( \frac{y}{1-y}\right) -\exp \left[ -\alpha -\theta \log \left( \frac{y}{1-y}\right) \right] \right\}$$
Cumulative distribution function $$F(y\mid\alpha,\theta)={\exp }\left[ -{{\exp }}\left( -\alpha \right)\left( \frac{1-y}{y}\right) ^{\theta } \right] $$
Quantile function $$Q(\tau \mid \alpha, \theta)= \frac{\left [-\frac{1}{\log(\tau) }\right ]^{\frac{1}{\theta}}}{\exp\left ( \frac{\alpha}{\theta} \right )+\left [-\frac{1}{\log(\tau) }\right ]^{\frac{1}{\theta}}}$$
Reparameterization $$\alpha = g^{-1}(\mu ) =\theta \log \left( {\frac{1-\mu }{\mu }}\right) +\log \left( -\frac{1}{\log \left( \tau \right) }\right)$$
where \(0<y<1\) and \(\theta >0\) is the shape parameter.
References
Mazucheli, J. and Alves, B., (2021). The unit-Gumbel Quantile Regression Model for Proportion Data. Under Review.
Gumbel, E. J., (1941). The return period of flood flows. The Annals of Mathematical Statistics, 12(2), 163--190.
Examples
set.seed(6969)
x <- rugumbel(n = 1000, mu = 0.5, theta = 1.5, tau = 0.5)
R <- range(x)
S <- seq(from = R[1], to = R[2], by = 0.01)
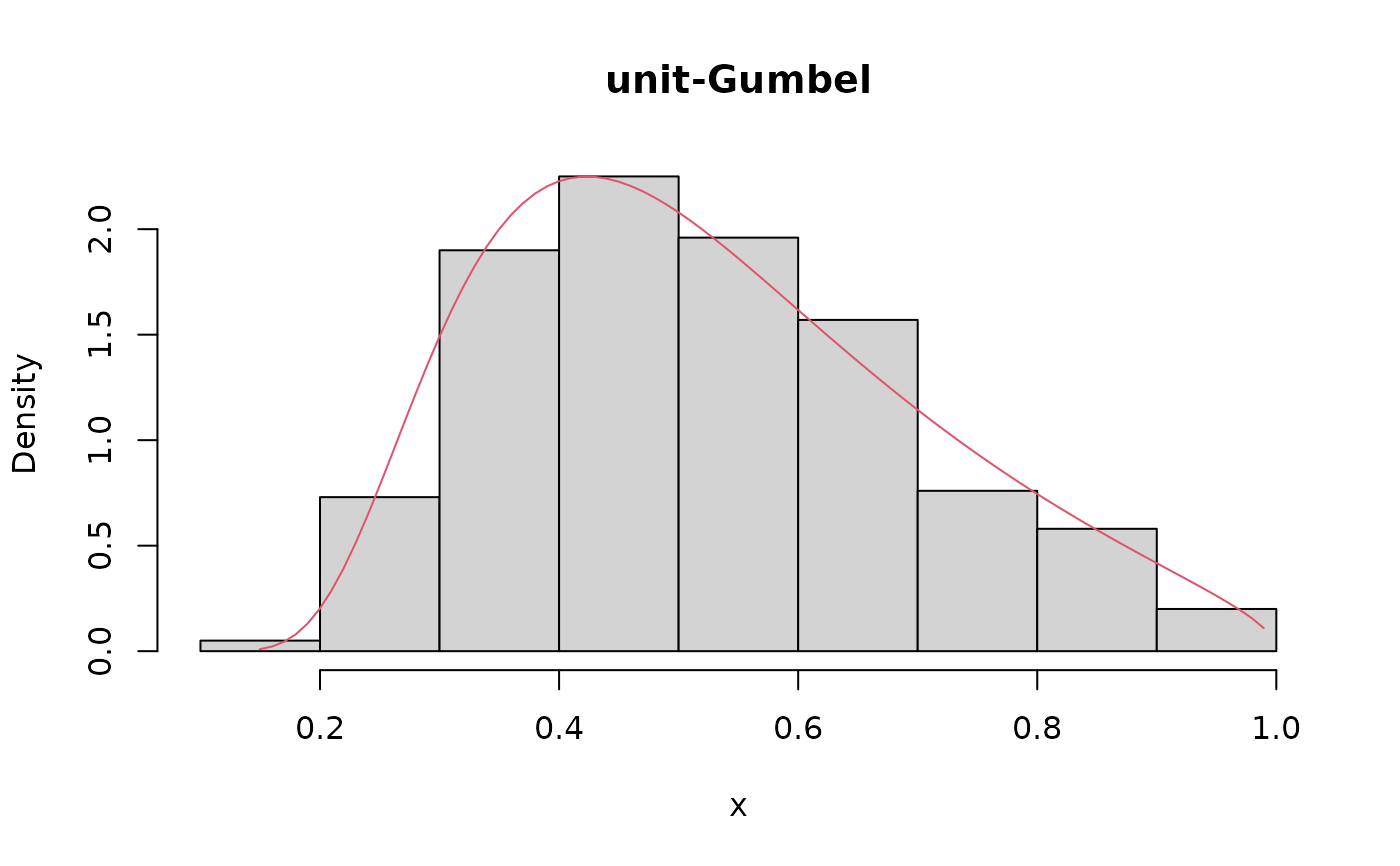
hist(x, prob = TRUE, main = 'unit-Gumbel')
lines(S, dugumbel(x = S, mu = 0.5, theta = 1.5, tau = 0.5), col = 2)
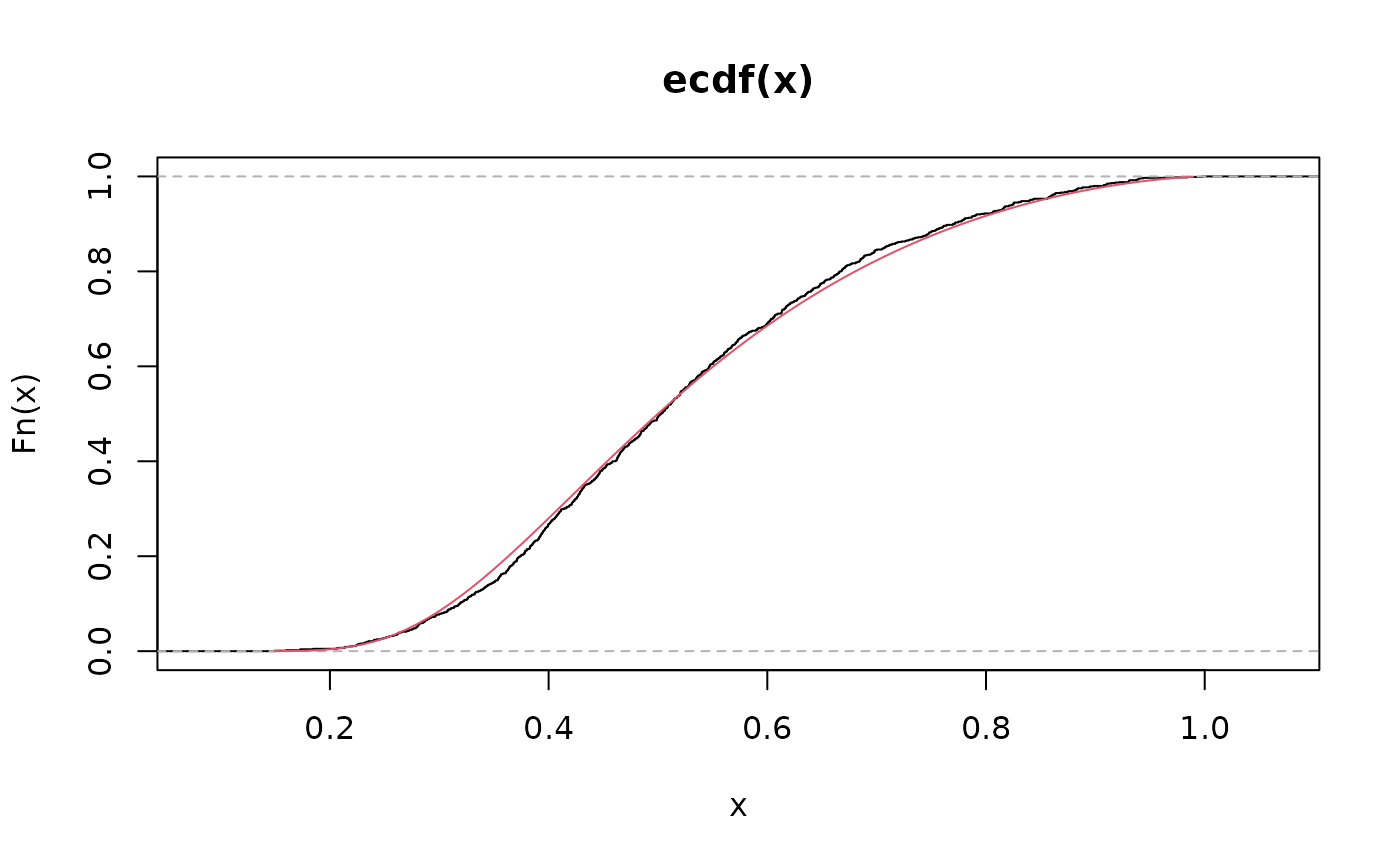
 plot(ecdf(x))
lines(S, pugumbel(q = S, mu = 0.5, theta = 1.5, tau = 0.5), col = 2)
plot(ecdf(x))
lines(S, pugumbel(q = S, mu = 0.5, theta = 1.5, tau = 0.5), col = 2)
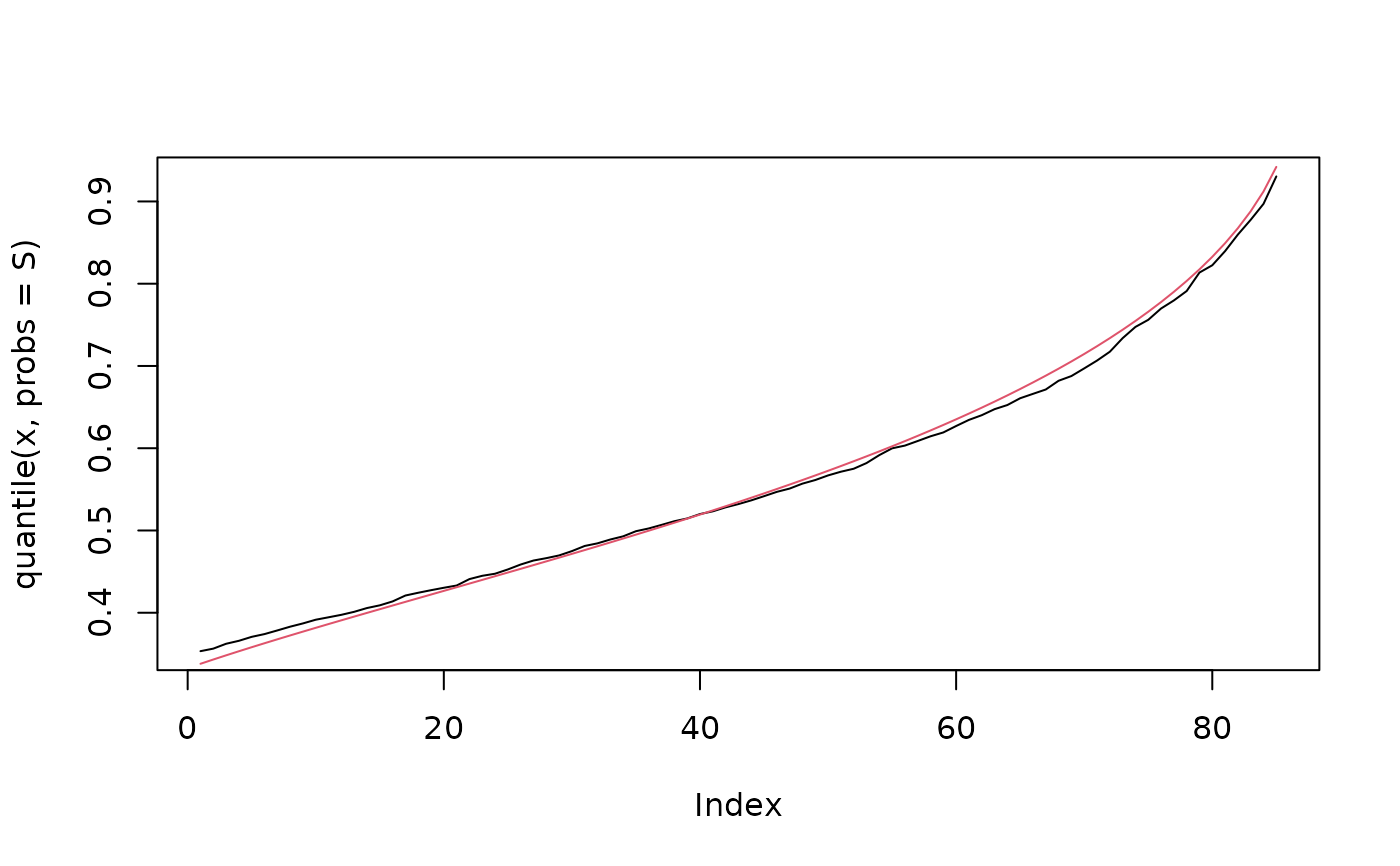
 plot(quantile(x, probs = S), type = "l")
lines(qugumbel(p = S, mu = 0.5, theta = 1.5, tau = 0.5), col = 2)
plot(quantile(x, probs = S), type = "l")
lines(qugumbel(p = S, mu = 0.5, theta = 1.5, tau = 0.5), col = 2)